Par Allie90
Mise à jour le 23-06-2014
Télécharger ce document
→ Téléchargement disponible après inscription
0,00/20
0 Avis > Donne ton avis
63 téléchargements
Ces exercices sont des exercices donnés par le jury sur le site internet du concours. Ils sont intéressants aussi bien en ENV A que en ENV B.
Grâce à notre professeur de mathématiques, Mlle Jovignot, vous serez en mesure de résoudre correctement ces exercices en suivant leur corrigé détaillé.
1. Montrer que la fonction F définie sur R par :
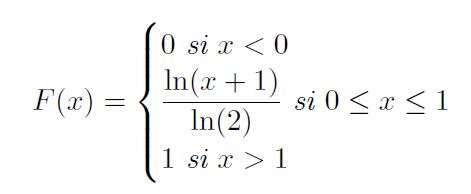
est la fonction de répartition d'une variable à densité notée X.
2. Soit k ∈ N* et t ∈ ]1, 1[. Calculer P (k ≤ 1/X ≤ k + t).
3. Soit Y = 1/X - E(1/X), où E(x) désigne la partie entière du réel x. Montrer que Y est une variable aléatoire de même loi que X.
On considère la matrice suivante :
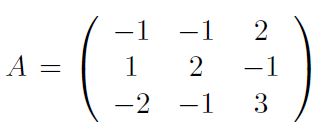
et on note Φ l'endomorphisme de R3 représenté par A dans la base canonique.
On note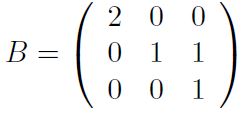 
1. Montrer que la matrice A n'est pas diagonalisable.
2. Soit v un vecteur propre de Φ associé à la valeur propre 1. Trouver un vecteur w de R3 tel que Φ(w) = v+w.
3. Montrer qu'il existe une matrice P inversible telle que B = P-1AP.
Télécharger ce document
L'ESIGETEL propose plusieurs recrutements allant de la prépa intégrée jusqu'aux concours (E3A et celui des BTS IUT) On peut y accéder en admission parallèle à Bac +2 ou +3 en 1ère année ou alors directement en 2ème année si on est Bac +4 cursus ingénieur.
Le MSc Ingénierie d’Affaires : une double compétence technologique et managériale pour manager les projets innovants du futur.
L’EPF est une école d’ingénieurs généralistes post-bac qui propose une formation d’ingénieurs généralistes, 2 formations binationales et une formation par apprentissage, toutes habilitées par la CTI.
www.epf.fr/
Les campus EXIA.CESI se trouvent dans 13 villes de France. On peut y suivre des formations de 5 ans sanctionnées par des diplômes homologués par l'Etat.
Ecole d'ingénieur post-bac fondée en 1936 et habilitée par la Cti depuis 1957, l'Efrei compte 7 000 diplômés et accueille près de 1200 élèves chaque année.
Questions / Réponses
EN DIRECT DES FORUMS
16777686 messages 16778261 réponses
