Vous devez être membre de digiSchool ingenieurs
ou Identifiez-vous :
Par LucieLagarde
Mise à jour le 19-05-2017
Télécharger ce document
→ Téléchargement disponible après inscription
0,00/20
0 Avis > Donne ton avis
432 téléchargements
Dans ce chapitre, nous allons voir la dernière notion liée aux fonctions dans ce programme de terminale S. Les intégrales vont nous permettre de calculer, en particulier, des aires. C’est une notion essentielle aussi bien pour les mathématiques que pour les sciences physiques. On sera également amené à parler dans cette fiche de primitives qui est aux fonctions ce que les fonctions sont aux dérivées. On réutilisera les intégrales quand on parlera de probabilités continues, également appelées probabilités à densité.
La notion d’intégration utilise tous les propriétés algébriques qui ont été vues jusqu’à présent sur les fonctions. Elle est très liée à la dérivation. Il est donc nécessaire de connaître toutes les formules de dérivation vues en 1S et cette année.
Télécharger le document pour voir cette partie
Définition
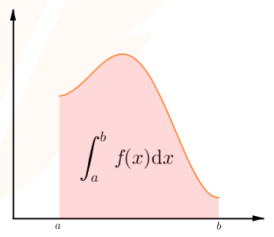
On considère une fonction f continue et positive sur un intervalle [a ; b].
L’aire, exprimée en unité d’aire, de la surface comprise entre :
Et on lit : « intégrale de a à b de f(x) dx ».
Remarques :
Télécharger le document pour voir cette partie
Voici un tableau reprenant les formules de dérivations vues cette année et en 1S mais lues dans un sens permettant de déterminer une primitive.
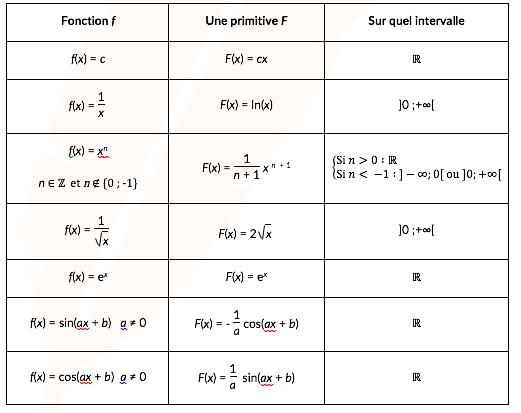
Voici un tableau reprenant les formules de dérivation des fonctions composées permettant de déterminer une primitive.

Télécharger le document pour voir cette partie
Propriétés
On considère deux fonctions f et g continues sur un intervalle I, trois réels a, b et c appartenant à l’intervalle I et un réel quelconque k.
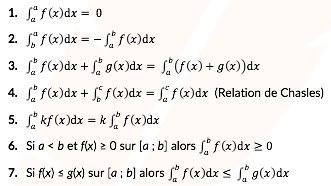
Télécharger le document pour voir cette partie

Télécharger le document pour voir la correction
I. Présentation II. Prérequis III. Et au concours IV. Intégrale d'une fonction continue et positive V. Primitives VI. Tableau de primitives VII. Lien entre intégrale et primitive VIII. Opérations sur les intégrales IX. Aire entre deux courbes X. Valeur moyenne XI. Exercice Geipi
Télécharger ce document


L’EPF est une école d’ingénieurs généralistes post-bac qui propose une formation d’ingénieurs généralistes, 2 formations binationales et une formation par apprentissage, toutes habilitées par la CTI.
www.epf.fr/
PIGIER, c'est un des plus grand réseaux d'écoles privées d'écoles techniques en France. De nombreuses formations sont disponibles dans toutes les grandes villes de France.
Ecole d'ingénieur post-bac fondée en 1936 et habilitée par la Cti depuis 1957, l'Efrei compte 7 000 diplômés et accueille près de 1200 élèves chaque année.
Ingésup est une école d'informatique qui propose un enseignement technologique, managérial et économique pour préparer au mieux les étudiants à un rôle d'expert et de manager dans l'entreprise.
Les campus EXIA.CESI se trouvent dans 13 villes de France. On peut y suivre des formations de 5 ans sanctionnées par des diplômes homologués par l'Etat.
Questions / Réponses
EN DIRECT DES FORUMS
16777689 messages 16778264 réponses

